Faktor–faktor yang mempengaruhi benda melakukan gerak parabola.

  • Benda tersebut bergerak karena ada gaya yang diberikan. Mengenai Gaya, selengkapnya kita pelajari pada pokok bahasan Dinamika (Dinamika adalah ilmu fisika yang menjelaskan gaya sebagai penyebab gerakan benda dan membahas mengapa benda bergerak demikian). Pada kesempatan ini, kita belum menjelaskan bagaimana proses benda‐benda tersebut dilemparkan, ditendang dan sebagainya. Kita hanya memandang gerakan benda tersebut setelah dilemparkan dan bergerak bebas di udara hanya dengan pengaruh gravitasi.
  • Seperti pada Gerak Jatuh Bebas, benda‐benda yang melakukan gerak peluru dipengaruhi oleh gravitasi, yang berarah ke bawah (pusat bumi) dengan besar g = 9,8 m/s2.
  • Hambatan atau gesekan udara. Setelah benda tersebut ditendang, dilempar, ditembakkan atau dengan kata lain benda tersebut diberikan kecepatan awal hingga bergerak, maka selanjutnya gerakannya bergantung pada gravitasi dan gesekan alias hambatan udara. Karena kita menggunakan model ideal, maka dalam menganalisis gerak peluru, gesekan udara diabaikan.

Gerak parabola merupakan suatu jenis gerakan benda yang pada awalnya diberikecepatan awal lalu menempuh lintasan yang arahnya sepenuhnya dipengaruhi oleh gravitasi.

Karena gerak parabola termasuk dalam pokok bahasan kinematika (ilmu fisika yang membahas tentang gerak benda tanpa mempersoalkan penyebabnya), maka pada pembahasan ini, Gaya sebagai penyebab gerakan benda diabaikan, demikian juga gaya gesekan udara yang menghambat gerak benda. Kita hanya meninjau gerakan benda tersebut setelah diberikan kecepatan awal dan bergerak dalam lintasan melengkung di mana hanya terdapat pengaruh gravitasi.

Gerak parabola disebut juga gerak peluru,mengapa dikatakan gerak peluru ? kata peluru yang dimaksudkan di sini hanya istilah, bukan peluru pistol, senapan atau senjata lainnya. Dinamakan gerak peluru karena mungkin jenis gerakan ini mirip gerakan peluru yang ditembakkan.

Contoh lintasan Gerak parabola

Dalam kehidupan sehari‐hari terdapat beberapa jenis gerak parabola.

Contoh 1.

Gerakan benda berbentuk parabola ketika diberikan kecepatan awal dengan sudut θ terhadap garis horisontal, sebagaimana tampak pada gambar di bawah.

Gambar 3 Ilustrasi lintasan benda bergerak parabola

Dalam kehidupan sehari–hari terdapat banyak gerakan benda yang berbentuk demikian. Beberapa di antaranya adalah gerakan bola yang ditendang oleh pemain sepak bola, gerakan bola basket yang dilemparkan ke ke dalam keranjang, gerakan bola tenis, gerakan bola volly, gerakan lompat jauh dan gerakan peluru atau rudal yang ditembakan dari permukaan bumi.

Contoh 2.

Gerakan benda berbentuk parabola ketika diberikan kecepatan awal pada ketinggian tertentu dengan arah sejajar horisontal, sebagaimana tampak pada gambar di bawah.

Gambar 4 Gambar peluru yang ditembakan mendatar dari suatu ketinggian

Beberapa contoh gerakan jenis ini yang kita temui dalam kehidupan sehari–hari, meliputi gerakan bom yang dijatuhkan dari pesawat atau benda yang dilemparkan ke bawah dari ketinggian tertentu.

Contoh 3.

Gerakan benda berbentuk parabola ketika diberikan kecepatan awal dari ketinggian tertentu dengan sudut teta terhadap garis horisontal, sebagaimana tampak pada gambar di bawah.

Gambar 5 Gambar peluru yang ditembakan dengan sudut elevasi tertentu dari suatu ketinggian

Dari penjelasan gerak parabola pada kehidupan sehari–haridiatas, gerak parabola memiliki ciri–ciri sebagai berikut:

1. Lintasan benda berupa parabola

2. Geraknya di udara

3. Memiliki kecepatan awal

4. Geraknya berada pada dua dimensi (x dan y). Benda yang bergerak dua dimensi tentu akan memiliki besaran–besaran vektor, begitu juga dengan gerak parabola.

Analisis Vektor Posisi dan Kecepatan

Coba kalian perhatikan gambar 6 di bawah ini! Sebuah benda mula-mula berada dipusat koordinat, dilemparkan ke atas dengan kecepatan awal {{V}_{0}} dan sudut elevasi {\alpha } . Pada arah sumbu X, benda bergerak dengan kecepatan konstan, atau percepatan nol (a=0), sehingga komponen kececpatan {{V}_{x}} mempunyai besar yang sama pada setiap titik lintasan tersebut, yaitu sama dengan nilai awalnya {{V}_{ox}} pada sumbu Y, benda mengalami percepatan gravitasi g.

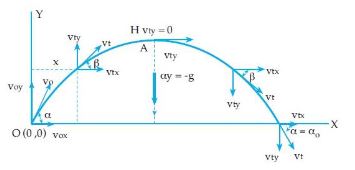
Gambar 6Lintasan parabola dari sebuah benda yang dilemparkan dalam arah αterhadap arah horizontal dengan kecepatan awal v0

Kecepatan benda pada Sumbu X dan Y di setiap titik

Titik O merupakan titik awal benda. Kecepatan pada titik ini merupakan kecepatan awal \left ( {{{V}_{0}}} \right ) untuk mencapai komponen kecepatan awal pada sumbu x \left ( {{{V}_{0x}}} \right ) dan komponen kecepatan awal pada sumbu y \left ( {{{V}_{0y}}} \right ) kita dapat menggunakan persamaan :

Gerak dalam arah sumbu X, berupa Gerak Lurus Beraturan (GLB), maka

    • Kecepatannya konstan, bukan fungsi waktu
      {{V}_{x}}={{V}_{0}}COS{\alpha }
    • Jarak dalam arah sumbu X dapat ditentukan dengan rumus
      X={{V}_{x}}t

Keterangan:
vx = kecepatan ke arah sumbu X (m/s)
v0 = kecepatan awal (v0)
X = jarak dalam arah sumbu X (m)
t = waktu (s)

Gerakan dalam arah sumbu Y, berupa Gerak Lurus Berubah Beraturan  maka

    • Kecepatan berupa fungsi waktu (berubah bergantung waktu)
      vy={{V}_{0}}sin{\alpha }-gt
    • Jarak dalam arah sumbu Y dapat ditentukan dengan rumus:
      Y={{V}_{0}}sin{\alpha }t-{{1}/{2}}\ {{gt}^{2}}

Keterangan :
Y = jarak dalam arah sumbu Y(m)
{{V}_{y}} = kecepatan ke arah sumbu y (m/s)
g = percepatan gravitasi \left ( {{{ms}^{2}}} \right )

Persamaan Gerak Parabola Dengan Analisis Vektor

Menurut analisis vector persamaan-persamaan gerak para bola dapat dituliskan sebagai berikut :

  • Posisi benda pada sembarang titik dalam waktu t dapat di tentukan dengan rumus :
    r = x i + y j
    r=\left ( {{{V}_{X}={{V}_{0}}cos{\alpha }}} \right )i+\left ( {Y={{V}_{0}}sin{\alpha }t-{{1}/{2}}{{gt}^{2}}} \right )j

    Keterangan :
    r = vektor posisi
    x = {{V}_{x}}t
    y = {{V}_{0}}sin{\alpha }t-{{1}/{2}}{{gt}^{2}}

  • Kecepatan benda pada sembarang titik dalam waktu t dapat ditentukan dengan rumus :
    V={{V}_{x}}i+{{V}_{y}}j

    Besar kecepatan pada sembarang titik adalah
    v={\sqrt {{{vx}^{2}}+{{vy}^{2}}}}

    Keterangan :
    v = vektor kecepatan
    {{V}_{x}}={{V}_{0}}cos{\alpha }
    vy={{v}_{0}}sin{\alpha }-gt

Contoh :

Dari titik A dari tanah, sebuah bola di lemparkan dengan kecepatan awal 20 m/s dan sudut elevasi 37º (sin 37º = 0,6) jika g = 10 m/s. hitunglah

a) KOmponen kecepatan awal dalam arah horisontal dan vertical
b) Kecepatan bola setelah 0,4 sekon
c) Posisi benda pada saat t = 0,4 sekon

Penyelesaian

 

Contoh :

Diketahui
{{V}_{0}}=20m/s,{\alpha }={{37}^{o}}dang=10m/{{s}^{2}}

a). Komponen kecepatan awal

Dalam arah horisontal

{{V}_{0x}}={{V}_{0}}cos{\alpha }
\left ( {20} \right )\left ( {cos{{37}^{o}}} \right )
= (20) (0,8)
= 16 m/s

Dalam arah vertikal
Voy = vo sin{\alpha }
= (20)(sin 370)
= (20) (0,6)
= 12 m/s

b). Kecepatan bola setelah 0,4s (t=0,4 s)

Kecepatan dalam arah horizontal tetap yaitu
Vx = v0x = 16 m/s

Kecepatan dalam arah vertikal yaitu
Vy = {{V}_{0y}} – gt = 12 – (10)(0,4) = 12 – 4 = 8 m/s

Dengan demikian diperoleh :
v={\sqrt {{vx}^{2}+{vy}^{2}}}
v={\sqrt {{12}^{2}+{8}^{2}}}
v=8 \surd 5\ m/s

c). Posisi bola setelah 0.4 sekon yaitu

Posisi bola arah horisontal
X={{V}_{x}}.t=\left ( {16} \right )\left ( {0,4} \right )=6,4\ m/s

Posisi bola arah vertikal
Y={{V}_{y}}-{{gt}^{2}}
={{V}_{y}}sin{\alpha }t-{{1}/{2}}{{gt}^{2}}
= 12(0,4) – 1/2 (10)(0,4){{}^{2}}
= 4,8 – 0,8
= 4 m

Jadi Posisi benda setelah 0,4 sekon berada pada koordinat (6,4m ; 4m)

Simulasi

Gerak Para Bola